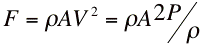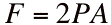Sat Jul 26 06:34:52 2025 GMT
What is a Water Rocket? |
|||
 A water rocket employs a
compressed gas to accelerate water through its nozzle as a means of
propulsion.
A water rocket employs a
compressed gas to accelerate water through its nozzle as a means of
propulsion.
The water inside the motor is essentially stationary and is accelerated to the velocity at the nozzle expressed by Burnouli's equation: Solving for Velocity:
The thrust is expressed by Newton's Second Law: 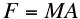 Where The Mass of the fluid flowing out of the nozzle in time dt is
Where A is the nozzle area. The Momentum (mass x velocity) is, therefore
If we neglect the relatively small velocity of the water inside the motor, we can say
that the momentum is gained entirely within time
by substituting for velocity from Eq. 1 above, or
|
|||
| updated 13-AUG-2007 |

Question? Comment? Send A Message

216.73.216.175
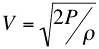
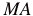 is the rate of change of momentum of the water being accelerated out of the nozzle.
is the rate of change of momentum of the water being accelerated out of the nozzle.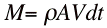
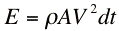
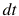 So the time rate of change of the momentum (thrust) is
So the time rate of change of the momentum (thrust) is